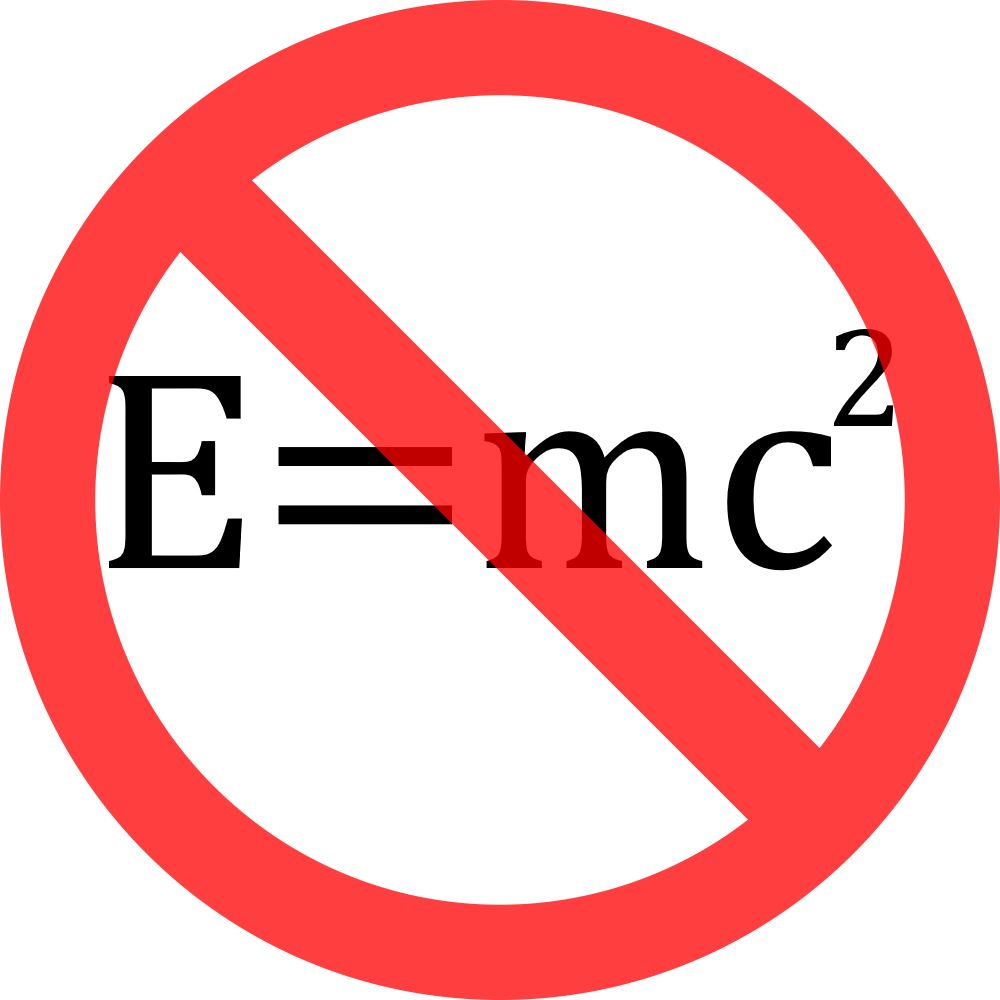
The titular formula is to many both the epitome and sum total of modern physics. It is regarded as the peak of human genius and the blueprint of the nuclear bomb.In some of these description, superlatives and awe seem to substitute for understanding. Surely, it covers blackboards in the lecture halls and offices of all reputable physics departments.
But surprisingly it does not. Even more surprising is the reason: this equation is universally agreed to be hogwash when the variables are interpreted in the way modern physicists find most convenient.That modern physicists know that \(c=1\) is a secondary reason for it merely renders the equation excessively verbose, rather than flatly wrong.
But that does not mean that modern physics rejects Einstein’s theories of relativity. Rather, it means that as physicists practiced relativity they discovered that the old-fashioned definitions of energy, mass, and momentum were inconvenient; unless one was extremely careful they readily led one into error. To avoid error and refocus mental effort away from the constant care needed to avoid that error, physicists just redefined the terms into a different, but much less error-prone form. Nothing was lost, for one could always at the end of the calculation, convert back to the old-fashioned definition. There was increasingly little need for that.
In particular, by \(m\) modern physicists always mean the body’s rest mass; what an observer moving with the body would measure as its mass. Rest mass is a Lorentz scalar. That means that any observer, regardless of relative location and velocity, will conclude that the body has the same numerical rest mass.
\(E\), however, is not a Lorentz scalar. Rather it is is first (or time-like) component of the four-dimensional energy-momentum vector. That means that it will be different for different observers. This is analogous to the x-component of a three-dimensional x-y-z vector. Then, if one rotated the coordinate system, the x, y, and z components of the vector would become mixed up. The Lorentz transformation of an t-x-y-z vector is (almost) exactly the same in principle and mixing formula.
So, if \(E\)—a component of a vector and different for different observers—was equal to \(m\)—a scalar and the same for every observer—times a constant \(c^2\),Which is of course exactly equal to \(1\). it would imply that the theory of relativity was wrong. As nobody believes such a silly thing, physicists universally disavow \(E=m c^2\) and even the equivalent \(E = m\).